Drawing a Circle With 2 Axis Robotics Math
This tutorial will teach you how to master inverse kinematics in 3D: the technique that solves the problem of moving a robotic arm to achieve for a specific target.
Y'all can read the rest of this online course here:
- Part 1. Changed Kinematics in 2nd: The Mathematics
- Part two. Inverse Kinematics in 2D: The Code
A link to download the unabridged Unity packet can be constitute at the finish of this tutorial.
Introduction
There are a few topics that keep recurring on this web log: one of them is, without whatsoever doubt, inverse kinematics. I have tackled this fascinating problem in two series and so far, for a full of 8 split up articles. And yet, there is still so much more to write almost changed kinematics in the context of video games.
What makes inverse kinematics then interesting and circuitous to require this many posts? The truth is that inverse kinematics is a problem that recurs not simply in video games, but in both engineering and science in general. From the blueprint of robotic arms to the understanding of motor control in the human brain, changed kinematics—in one form or another—plays an important role.
A Brief Summary
The first series defended to the topic, An Introduction to Procedural Animations, came out in 2017 and further popularized the term "procedural animations" among indie developers. It provided a general solution based on a gradient descent algorithm, which could potentially be used on rather "exotic" riggings, such equally tentacles and spider legs.
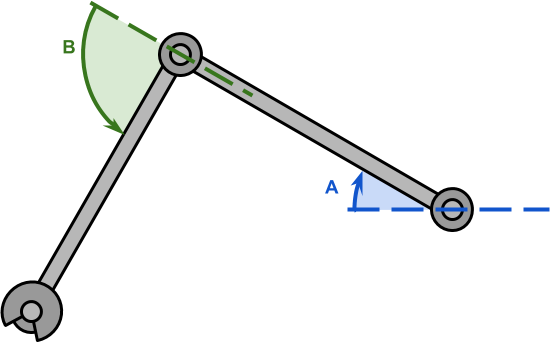
The second serial, Inverse Kinematics in 2d, came out 1 year afterwards and focused on a very specific case: a ii-joint arm constrained in a 2nd plane (below). Exactly equally the proper noun suggested: inverse kinematics in 2d. Each one of the two joints is controlled by an angle, ![]() and
and ![]() . By modulating these two angles, the tip of the robotic arm, called the end effector, will reach different locations.
. By modulating these two angles, the tip of the robotic arm, called the end effector, will reach different locations.
The problem of inverse kinematics is to find the angles ![]() and
and ![]() and then that the end effector reaches a desired target point. The animation below shows a robotic arm that is drawing a circle, aligned on the XY airplane.
and then that the end effector reaches a desired target point. The animation below shows a robotic arm that is drawing a circle, aligned on the XY airplane.
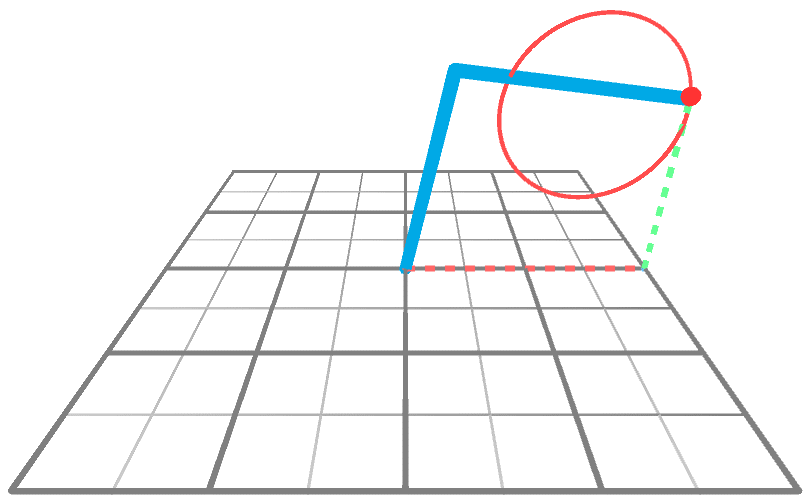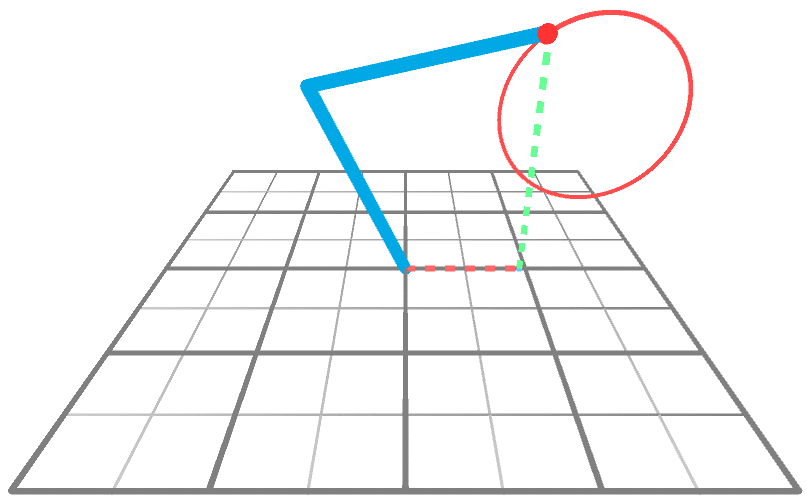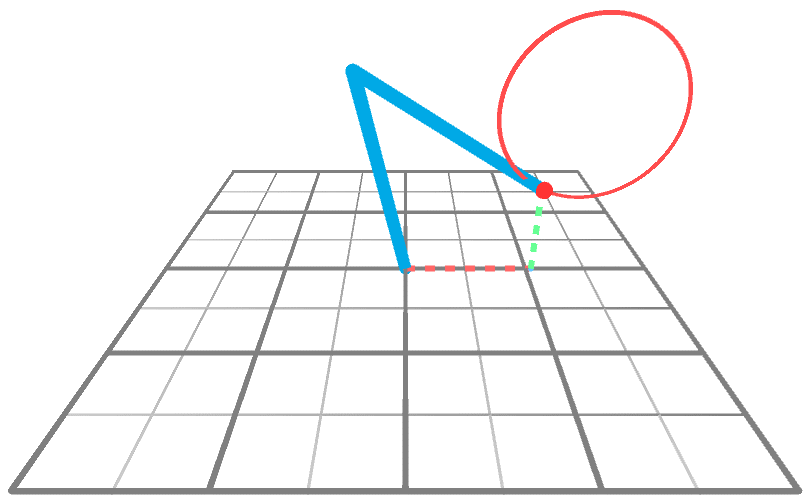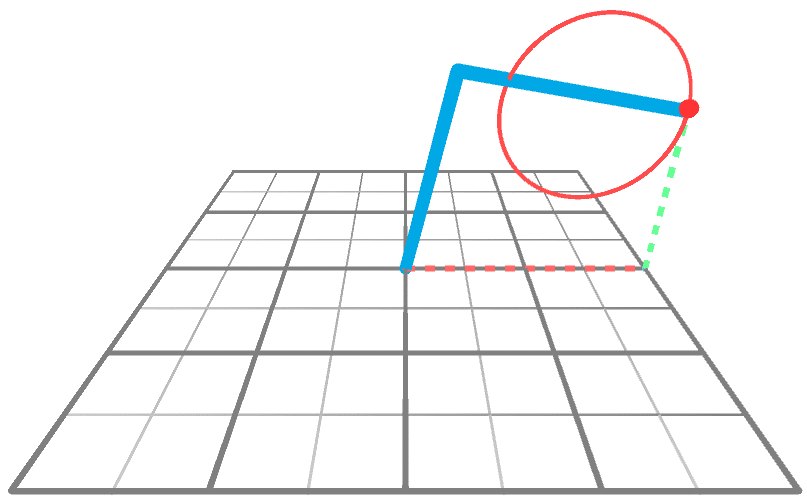
Technically speaking, the solution presented on Inverse Kinematics for Robotic Arms can work with potentially whatever number of joints. So why focusing on a less powerful technique? The answer is simple: efficiency. What made this worth writing most was the fact that, in the specific scenario just described, a solution tin can be found using a simple equation instead of a rather complex algorithm. That is thank you to the fact that we can imagine the robotic arm as a triangle (beneath) with two internal angles ![]() and
and ![]() .
.
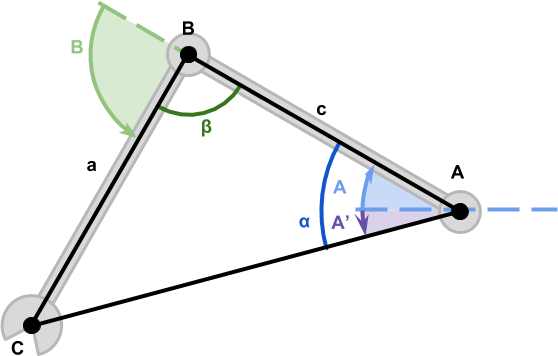
With a little bit of trigonometry, nosotros establish out the values for such angles to exist:
(i) ![]()
(2) ![]()
where ![]() ,
, ![]() and
and ![]() are the sides of this "imaginary" triangle that nosotros constructed.
are the sides of this "imaginary" triangle that nosotros constructed.
However, the joints of the robotic arm are controlled using ![]() and
and ![]() , which turns out to exist:
, which turns out to exist:
(three) ![]()
(4) ![]()
where:
(v) ![]()
📚 Prove me the derivation!
The total derivation can be constitute in the commodity titled Inverse Kinematics in 2D: The Mathematics.
Extending into the Third Dimension
If yous have followed the Changed Kinematics in 2nd series before, there should non exist anything new in the previous section. If you have non, do non worry: that is all you demand to know.
What makes that simplified case worth discussing, is that it can be used as the starting point for solving inverse kinematics in 3D.
First of all, we demand to understand that the scenario of a two-joint arm in 2nd is a problem with two degrees of freedom (2DOF). Conversely to what i might imagine, it does non hateful that nosotros take 2 segments; but that we accept command over ii variables (which, in this case, turns out of to be the joint angles).
When we extend this problem to the third dimension, our robotic arm all the same has two segments and two joints. However, the problem has now three degrees of freedom (3DOF), if we assume that we tin can also rotate the arm freely around its first joint.
Under this new scenario, the 2nd joint (![]() ) remains unchanged. However, nosotros assume that the beginning ane (
) remains unchanged. However, nosotros assume that the beginning ane (![]() ) can now freely rotate in another dimension. Because of this, the starting time joint is frequently referred to every bit the hip, and the second every bit the articulatio genus. Your knee joint has generally just ane degree of freedom (forwards/backwards), while your hip has two (forwards/backwards and inwards/outwards). The bending around which the hips rotates is indicated with
) can now freely rotate in another dimension. Because of this, the starting time joint is frequently referred to every bit the hip, and the second every bit the articulatio genus. Your knee joint has generally just ane degree of freedom (forwards/backwards), while your hip has two (forwards/backwards and inwards/outwards). The bending around which the hips rotates is indicated with ![]() .
.
We can imagine a robotic arm in which both joints can have ii degrees of liberty, for a full of 4. The trouble at that indicate is that there will be multiple solutions, making our approach non effective anymore. "Leg-like" robotic arms (meaning: artillery that have a hip and a knee joints) are very common both in games and in the manufacture in general. So this approach is probably worth studying.
If you have read the previous articles, you might think that if the target is reachable in 2d, there are always two "specular" solutions (below).
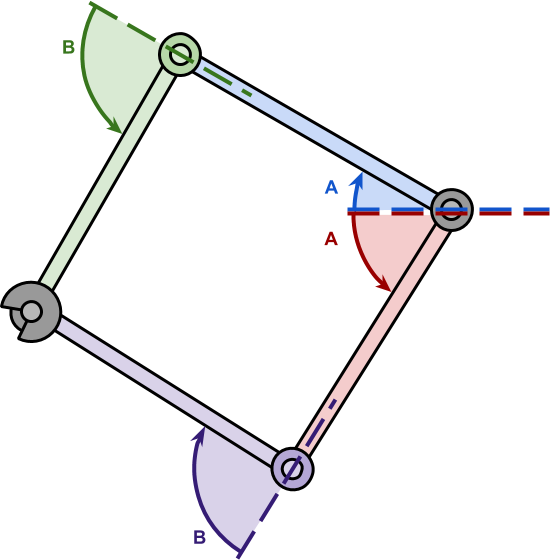
The aforementioned trouble occurs in 3D; this time, the solutions are infinite. This is considering the configuration tin can rotate effectually the axis of symmetry represented by the direct line that connects the origin from the target. The solution is to… focus on simply i solution! In this tutorial, nosotros volition focus on the most simple to find, which assumes (0, 1, 0) as the "upwardly" management.
From 2D to 3D
So far, we only know how to solve the trouble of inverse kinematics when the movement is constraints to the XY airplane. The trick to get from 2d to 3D is to re-use the 2d solution. The blitheness below shows a robotic arm reaching for a bespeak in 3D infinite, which revolves around the Y-axis. Information technology is pretty obvious to see that the simply matter the arm does is to revolve too; its angles ![]() and
and ![]() are not changing, simply
are not changing, simply ![]() does.
does.

This means that, if nosotros know how to perform IK on the XY aeroplane (and we do!) we know how to perform information technology on the entire XYZ space with two unproblematic rotations. Conceptually, we can solve the problem in three steps:
- Rotate the target betoken around the Y-centrality, until it lies on the XY aeroplane
- Motion the robotic arms so that it can reach for the indicate, equally if it was in 2D
- "Undo" the rotation by rotating the entire robotic arm in the reverse direction on the Y-axis.
We can do this more than efficiently by just performing the 2D changed kinematics not on the XY plane, only on the vertical plane passing from the root of the robotic arm to the target point.
Rotation Around Y-Axis
To perform changed kinematics in 3D, the offset matter that we demand to calculate is ![]() , which is the angle around which the entire robotic arm revolves. This is the extra degree of freedom added to the hip joint.
, which is the angle around which the entire robotic arm revolves. This is the extra degree of freedom added to the hip joint.
The best mode to find it, is to assume that the robotic arm has already reached the position (meaning that ![]() is already at the target position) and calculating the resulting angle
is already at the target position) and calculating the resulting angle ![]() . Since
. Since ![]() is the bending fabricated by the hip around the Y-axis, we tin look at the robotic arm straight from the pinnacle. With a tiptop-downwardly view over the XZ airplane (below), the robotic arm looks like a straight line. This is because, exception made for the hip, the other ii joints are constraints on a airplane.
is the bending fabricated by the hip around the Y-axis, we tin look at the robotic arm straight from the pinnacle. With a tiptop-downwardly view over the XZ airplane (below), the robotic arm looks like a straight line. This is because, exception made for the hip, the other ii joints are constraints on a airplane.
If we look at the segment ![]() equally the hypothenuse of a right triangle, we can use a scrap of trigonometry to calculate the bending
equally the hypothenuse of a right triangle, we can use a scrap of trigonometry to calculate the bending ![]() :
:
(vi) ![]()
📚 Evidence me the derivation!
Computing the angle between two points is a pretty common trouble for game developers, which can exist solved hands with a flake of trigonometry.
The trick, in this case, is to introduce the gradient of a line (beneath), which is the ratio between its ascension (![]() ) and run (
) and run (![]() ). The slope of a line can exist calculated between any two given, distinct points, and it yields the same result.
). The slope of a line can exist calculated between any two given, distinct points, and it yields the same result.

The slope of a line has a directly relationship with the bending of the line ![]() :
:
(vii) ![]()
If you take studied trigonometry, you should in fact recognise that the rise ![]() is in fact
is in fact ![]() and the run
and the run ![]() is
is ![]() . And the tangent office is, by definition, the ration between sine and cosine.
. And the tangent office is, by definition, the ration between sine and cosine.
To extract ![]() from (7) we tin can use the changed tangent function, which is known as arctangent:
from (7) we tin can use the changed tangent function, which is known as arctangent:
(8) ![]()
While this works really nice in theory, at that place are a few issues with the sign of ![]() and
and ![]() . The slope, in fact, yields the same effect when
. The slope, in fact, yields the same effect when ![]() and
and ![]() are both positive or both negative. Just, from a geometrical signal of view, those correspond to two reverse angles! The solution is to not utilise
are both positive or both negative. Just, from a geometrical signal of view, those correspond to two reverse angles! The solution is to not utilise ![]() directly, just its "programming" cousin,
directly, just its "programming" cousin, atan2. Most frameworks have an implementation of the arctangent function that takes 2 parameters, usually called dy and dx.
⭐ Suggested Unity Avails ⭐
Unity is free, but you can upgrade to Unity Pro or Unity Plus subscriptions plans to get more functionality and training resources to power up your projects.
Inverse Kinematics on the WY Plane
Technically speaking, knowing ![]() is more than enough to solve inverse kinematics in 3D. What nosotros could practice, in fact, is to follow the algorithm presented in the previous section: rotating the target betoken by
is more than enough to solve inverse kinematics in 3D. What nosotros could practice, in fact, is to follow the algorithm presented in the previous section: rotating the target betoken by ![]() degrees effectually the Y axis, performing the inverse kinematics on the XY airplane, and finally rotating the entire arm by
degrees effectually the Y axis, performing the inverse kinematics on the XY airplane, and finally rotating the entire arm by ![]() degrees.
degrees.
A quicker version is to perform the inverse kinematics not on the 2nd plane, but directly on the vertical plane passing through the hip articulation and the target point. At that place is, unfortunately, something that is preventing u.s.a. from doing and then. Let'southward look one time again at the diagram which indicates all of the angles used:

In order to calculate ![]() , which is the angle that controls the first joint, nosotros need to calculate
, which is the angle that controls the first joint, nosotros need to calculate ![]() . That is the angle betwixt the offset articulation and the target signal, If we recall equation (5) used to calculate
. That is the angle betwixt the offset articulation and the target signal, If we recall equation (5) used to calculate ![]() , we find one big problem: information technology assumes all points lie on the XY airplane:
, we find one big problem: information technology assumes all points lie on the XY airplane:
![]()
In our 3D scenario, unfortunately the robotic arm would be rotated past ![]() degrees around the Y-axis. The new diagram stays mostly the aforementioned, however, if nosotros rotate our view together with the robotic arm. We phone call this new reference frame WY, since the X-axis is now replaced by W, which was the X-axis, not rotated past
degrees around the Y-axis. The new diagram stays mostly the aforementioned, however, if nosotros rotate our view together with the robotic arm. We phone call this new reference frame WY, since the X-axis is now replaced by W, which was the X-axis, not rotated past ![]() degrees around the Y-centrality.
degrees around the Y-centrality.

We cannot simply do ![]() as we did for
as we did for ![]() . This is because while
. This is because while ![]() and
and ![]() are aligned on the Y-axis,
are aligned on the Y-axis, ![]() and
and ![]() are not aligned to the X-axis. They are aligned to the Westward-axis. The best mode to calculate
are not aligned to the X-axis. They are aligned to the Westward-axis. The best mode to calculate ![]() is, consequently, to become the distance from
is, consequently, to become the distance from ![]() to
to ![]() . This loses the sign of
. This loses the sign of ![]() , but it luckily bears no real result on our calculations. If your arm happens to motility in the opposite management, simply flip the sign of
, but it luckily bears no real result on our calculations. If your arm happens to motility in the opposite management, simply flip the sign of ![]() in your code.
in your code.
(9) 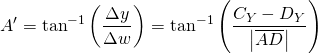
where ![]() is the length of the segment from
is the length of the segment from ![]() to
to ![]() . Information technology tin be calculated hands with a role such every bit
. Information technology tin be calculated hands with a role such every bit Vector3.Altitude, or you could also use Pythagoras' theorem directly:
(x) 
In the equation in a higher place, the Y contribution from the Pythagoras' theorem cancels itself out because the signal ![]() has the same Y component of
has the same Y component of ![]() , then their
, then their ![]() is zero.
is zero.

Now, we really exercise have everything to perform changed kinematics in 3D for robotic arms with i dandy and hip articulation:
(11) ![]()
(12) 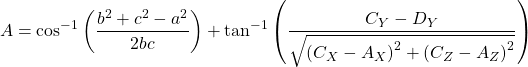
(13) ![]()
While looking scary, these equations are simple to implement and allows to perfom inverse kinematics in 3D as fast as possible.
What'southward Next…
The next tutorial in this serial will evidence how to employ inverse kinematics to create conceivable legged creatures. Yes, the anticipated tutorial about changed kinematics for spider legs is finally coming!!!

Unity Parcel Download
Get a Patron!
You lot can download all the avails used in this tutorial to have a fully functional robotic arm for Unity.
| Feature | Standard | Premium |
| Changed Kinematics in 3D | ✅ | ✅ |
| Multiple Solutions | ❌ | ✅ |
| Shine Reaching | ❌ | ✅ |
| Test Scene | ❌ | ✅ |
| Test Animations | ❌ | ✅ |
| Download | Standard | Premium |
Additional Resources
- Changed Kinematics (two joints) for foot placement
- Elementary 2 Joint IK
- 3D Inverse Kinematics
💖 Back up this blog
This websites exists thank you to the contribution of patrons on Patreon. If you recall these posts have either helped or inspired you, delight consider supporting this weblog.

📧 Stay updated
You will be notified when a new tutorial is relesed!
📝 Licensing
You are gratis to use, adapt and build upon this tutorial for your own projects (even commercially) equally long as you credit me.
You are not allowed to redistribute the content of this tutorial on other platforms. Especially the parts that are only available on Patreon.
If the knowledge you lot have gained had a significant impact on your project, a mention in the credit would be very appreciated. ❤️🧔🏻
Source: https://www.alanzucconi.com/2020/09/14/inverse-kinematics-in-3d/